Перспективы (пост)квантовой криптографии: есть место для секретов!
Тишину любят не одни только деньги — веками секретность и непубличность оставались важнейшими атрибутами дипломатических, к примеру, сношений. Последствия заключаемых между странами договоров ощущали на себе миллионы их жителей, однако точные формулировки и дополнительные условия этих соглашений нечасто становились широко известны. Достаточно вспомнить, какую бурю на международной арене вызвало предание большевиками в 1917 г. гласности тайных договоров, заключавшихся царским, а затем и Временным правительством. Правда, взятый изначально Советской властью курс на полную прозрачность даже в области дипломатии, не говоря уже о делах военных и финансовых, выдерживался недолго: стало понятно, что сохранение тайны замыслов, договорённостей и приказов принципиально важно для существования государства как такового.
И если личные переговоры можно провести в тщательно обследованном и защищённом от прослушивания помещении, а протоколы по их итогам запрятать в сейфы с хитроумными замками, как быть с обменом данными на расстоянии? Перехват депеш — не только дипломатических — давно практикуемый способ проникновения в чужие секреты, и естественным ответом на него стало шифрование сообщений. Которое, правда, породило другую проблему: раз шифр известен по меньшей мере двум сторонам (источнику и получателю), вполне вероятна его утечка. И даже в предположении, что та крайне маловероятна, закодированная депеша всё равно хранит ценную информацию — а значит, будучи перехваченной, потенциально может быть расшифрована даже при отсутствии у заинтересованной третьей стороны изначальных знаний о системе кодирования.

К концу XIX века лондонская пневмопочта доросла до пересылки грузов в тележках по чугунным трубам диаметром около 800 мм со стенками дюймовой толщины (источник: The Postal Museum)
Защитить как можно надёжнее канал передачи от перехвата реально лишь на крайне ограниченных расстояниях, причём не обязательно с применением самоновейших технологий. Так поступили, например, в офисе канцлера ФРГ, где решили не демонтировать старинную пневмопочту, используемую уже более ста лет для переправки чувствительных бумажных документов между самим главой исполнительной власти и его наиболее высокопоставленными сотрудниками, — как раз в стремлении снизить риски возможного перехвата. Правда, общая протяжённость берлинской двухпутной пневмопочтовой системы с 36 станциями не превышает 1,3 км, так что внутри здания канцелярии она вполне себя оправдывает, а вот в масштабах даже отдельно взятого города, не говоря уже о стране, в принципе неприменима. Есть и другой подход: вместо проверенных временем аналоговых использовать наиболее передовые квантовые технологии — как это делают, скажем, в КНР, где запущенный ещё в 2016-м «квантовый спутник» Mozi обеспечивает зашифрованные мультимедийные коммуникации буквально через пол-Евразии.
Квантовые средства шифрования — точнее, доставки шифровальных ключей — представляются на сегодня наиболее надёжными в плане устойчивости к взлому. В то же время немалая доля алгоритмов, широко применяемых при кодировании данных, потенциально уязвимы перед грядущими квантовыми компьютерами — поскольку те смогут выполнять определённые математические операции, необходимые для взлома таких шифров, на несколько порядков быстрее самых производительных фоннеймановских машин. В результате квантовые технологии, с одной стороны, применяют для обмена ключами посредством передачи и приёма квантовых объектов (чаще всего фотонов) — это собственно квантовая криптография. С другой стороны, угроза со стороны пока не реализованных 1000-кубитных и ещё более масштабных квантовых компьютеров заставляет разработчиков заранее подыскивать новые алгоритмы шифрования сообщений — это уже постквантовая, или квантово-безопасная, криптография. Познакомимся с обоими этими подходами к защите информации поближе.

«Квантовый спутник» Mozi назван в честь древнекитайского философа Мо-цзы, одного из последователей и переосмысливателей Конфуция (источник: Chinese Academy of Science)
Изначально системы шифрования в целом делились на перестановочные и подстановочные (гибридные методы с использованием обоих подходов также, впрочем, не исключены). Перестановочные системы сохраняют фрагменты исходного текста — отдельные буквы и цифры, слоги, слова, — но меняют их местами так, что для стороннего читателя связное сообщение превращается в бессмысленную последовательность текстовых элементов. Древнейшая из достоверно зафиксированных (ок. 400 г. до н. э.) практик применения перестановочного шифрования — спартанские скиталы (от греческого σκυτάλη, «жезл»), сужающиеся к одному из концов деревянные бруски, на которые плотно, виток встык витку, наматывалась узкая пергаментная или кожаная лента. На этой ленте вдоль скиталы, строка за строкой, каждая буква на своём витке, открытым текстом записывали сообщение. После чего ленту разворачивали и переправляли с курьером адресату, располагавшему точно такой же скиталой для дешифровки. Прочесть же перехваченную депешу, не имея бруска нужного переменного сечения, не было практически никакой возможности — особенно в отсутствие компьютеров, способных методом прямого перебора быстро выявить все возможные комбинации букв на ленте с сообщением. Есть даже указания на использование перестановочной криптографии в Древнем Египте и Месопотамии за 1,5-2 тыс. лет до н. э., но они довольно туманны.

Реконструкция спартанской скиталы с намотанной на неё лентой сообщения (источник: Wikimedia Commons)
Чуть позже, на закате республиканского Рима, не кто иной, как Юлий Цезарь, изобрёл названный его именем подстановочный шифр, подразумевавший замену каждого символа в сообщении другим по определённому и очень простому правилу. В оригинале каждая буква латинского алфавита всего лишь сдвигалась на три позиции: S превращалась в V, E в H и т. д. Уже в компьютерную эпоху (и в основном в дидактических целях, как одна из задачек для начинающих программистов) был предложен шифр ROT13: всё как у Цезаря, но сдвиг производится сразу на 13 позиций. Для английского алфавита из 26 букв это означает, что два последовательных сдвига вправо на 13 символов превращают исходную букву в саму себя, что избавляет программиста от необходимости вводить отдельную процедуру сдвига влево для дешифровки. Впрочем, в случае архаичной латыни с её 20 буквами и даже классической с 23 этот метод бы не сработал.
Число позиций сдвига в шифре Цезаря является криптографическим ключом: той самой секретной (для всех, кроме отправителя и получателя) информацией, что позволяет и зашифровать, и расшифровать сообщение. Поскольку в ранних системах такого рода один и тот же ключ применялся обеими сторонами кодированной коммуникации, эти системы получили название симметричных. И если шифр Цезаря представляется достаточно тривиальным — по крайней мере, ключ его выявляется методом последовательного перебора за считаные миллисекунды после написания и запуска несложной программы, — то современные симметричные алгоритмы шифрования, наиболее известный среди которых носит название AES, уже не так-то просто взломать даже при наличии мощного суперкомпьютера. В их основе лежит блочное шифрование: подстановки и перестановки, причём по весьма нетривиальной схеме, производятся не на обычном буквенном алфавите, а на алфавите блоков, каждый из которых состоит из определённого числа символов (часто из 128).

Пример практичного устройства для кодирования и раскодирования сообщений, записанных шифром Цезаря (источник: CaesarCipher.Net)
Сама процедура симметричного шифрования предусматривает применение различных математических преобразований. Простой сдвиг по алфавиту — простейший вариант, тогда как алгоритмы вроде AES, его предшественника DES и пр. включают многократное циклическое использование сдвигов по предварительно составленному алфавиту блоков, сложений байтов по определённому модулю, применение к ним побитового исключающего логического «ИЛИ» (XOR) и т. п. При этом алгоритм шифрования остаётся открытым, известным не только передающей и принимающей сторонам, но и любому потенциальному злоумышленнику, который мог бы стремиться перехватить и декодировать зашифрованное сообщение, — и только ключ является единственным по-настоящему секретным элементом коммуникации. Такой подход вполне оправдан в соответствии с эмпирическим правилом Керкхоффа (по имени автора изданного в конце XIX века труда «Военная криптография», в котором оно было впервые сформулировано, — Огюста Керкхоффа, Auguste Kerckhoffs): «Доступ противника к криптографической системе не должен иметь неприятных последствий». Иными словами, принципы шифрования с ключом должны быть настолько надёжны, чтобы даже попадание в руки злоумышленника самой шифровальной машины в отсутствие ключа не помогло бы ему декодировать перехваченное сообщение.
Предельным случаем реализации симметричного шифрования можно считать шифр Вернама (Gilbert S. Vernam, американский инженер и телеграфист, в 1919 г. запатентовавший автоматическую систему для шифрования телеграфных сообщений) — принципиально невзламываемый за счёт того, что длина применяемого в нём ключа шифрования равна длине кодируемого сообщения или даже превосходит её, а сам этот ключ представлен абсолютно случайным и уникальным, используемым лишь однократно, набором символов. Именно отсутствие всякой системы в ходе шифрования (реализуемого для шифра Вернама через свёртку исходного текста с ключом посредством простейшей логической функции XOR) в сочетании с однократностью применения каждого ключа делает сообщение неуязвимым для криптоаналитики — поиска внутренних закономерностей предполагаемого алгоритма кодирования. Значительная же длина самого ключа не просто затрудняет «грубый» взлом методом последовательного перебора всех возможных вариантов, но ещё и даёт шанс запутать злоумышленника. Ведь в процессе такого перебора вполне может случайно отыскаться ложный ключ, который преобразует кодированное сообщение во вполне осмысленный текст — правда, совсем не тот, что был изначально зашифрован.

Американская шифровальная машина SIGTOT для кодирования телеграфных сообщений с одноразовым ключом-перфолентой, 1917 г. (источник: Cipher Machines)
Теоретически едва ли не идеальный, на практике шифр Вернама сегодня применяется чрезвычайно редко — как раз по причине того, что для каждого обмена сообщениями в его случае необходим свой уникальный ключ размером не меньше самой шифруемой депеши. Стоит задействовать один и тот же ключ хотя бы дважды — и у злоумышленника моментально появляется ненулевая возможность произвести успешный взлом, используя криптоанализ. Но как снабдить отправителя и получателя строго идентичными наборами одноразовых ключей, заведомо не подвергая последние опасности перехвата? Классическое решение этой задачи — физические (бумажные) шифроблокноты с предварительно сгенерированными ключами, использованные страницы которых сразу же уничтожаются, слишком громоздки, да и скопировать их удачливый агент потенциально сможет. А передавать ключ длиной с само сообщение (а то и больше) по гипотетическому заведомо защищённому сверхнадёжному каналу связи смысла нет — раз уж такой канал имеется, проще использовать его для трансляции самой депеши открытым текстом.
В итоге главной проблемой современной криптографии становится налаживание такого заведомо защищённого канала, пусть даже с крайне невысокой пропускной способностью, по которому можно передать сравнительно короткое сообщение — ключ шифрования, с которым затем принимающая сторона сможет раскодировать депешу любого необходимого размера, полученную уже по недоверенному широкому каналу. Частично эту задачу решает асимметричное шифрование, при котором вместо одного ключа генерируется исходно два: открытый, который передаётся по недоверенному каналу, и закрытый, применяемый лишь для раскодирования сообщения. Алгоритм получения открытого ключа из закрытого сравнительно прост, тогда как обратная задача «в лоб» практически неразрешима (прямая аналогия с разложением большого числа на простые множители). В асимметричной схеме будущий получатель секретной информации (не отправитель!) генерирует у себя пару ключей, открытый ключ переправляет отправителю, тот зашифровывает с его помощью сообщение и — вновь по недоверенному каналу — высылает шифровку получателю. Даже перехватив открытый ключ и саму депешу, злоумышленник не сможет за разумное время (если корректно выбран алгоритм шифрования, конечно же) получить вожделенные данные. Современные системы шифрования, применяемые буквально повсеместно — от авторизации на различных веб-сайтах и проведения банковских транзакций до шифрования потоковых мультимедиаданных и обмена сообщениями по каналам спецсвязи — комбинируют, как правило, симметричные и асимметричные схемы.
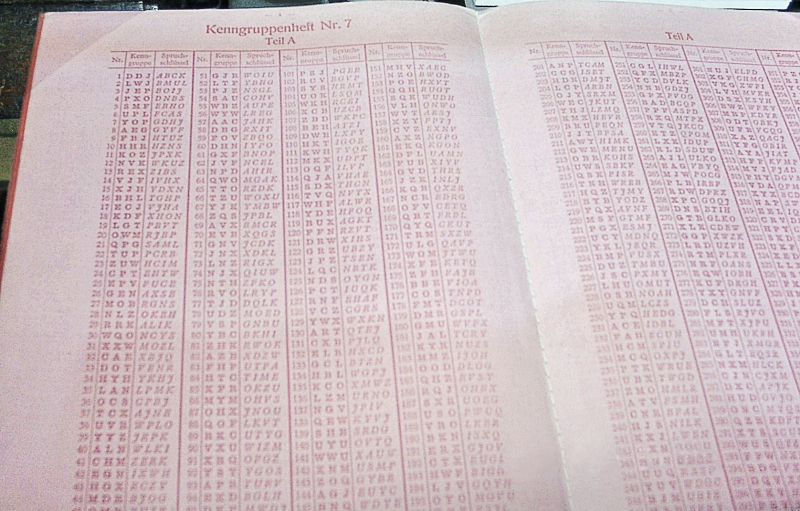
Kenngruppenheft — кодовая книга с ключами для расшифровки кодированных радиограмм с применением машины Enigma, выдававшаяся экипажам Кригсмарине (источник: Wikimedia Commons)
Главная загвоздка с шифрованными коммуникациями на расстоянии — в том, что чем больше дистанция между отправителем и получателем, тем труднее гарантировать отсутствие активного вмешательства злоумышленника в криптографический процесс. Противодействовать пассивному перехвату сообщений современные системы шифрования позволяют вполне неплохо (ведь скопировать шифровку мало — приходится тратить время и ресурсы на декодирование), однако каждое применение асимметричной схемы неизбежно порождает риск злонамеренной подмены данных в канале передачи. «Человеку посредине» — man-in-the-middle, MITM — нетрудно перехватить передаваемый получателем по недоверенному каналу открытый ключ. После чего злоумышленник технически может заблокировать дальнейшую переправку легитимного сообщения, — а затем создать новую шифровку уже со своими открытым и закрытым ключами, переслав её отправителю вожделенных секретных данных. Получив и расшифровав депешу отправителя, MITM волен вновь зашифровать её с легитимным открытым ключом получателя и переправить последнему. В результате время на прохождение депеши чуть увеличивается, но, помимо этого, никаких средств обнаружить компрометацию канала связи (подмену открытого ключа) у отправителя и получателя нет — особенно если злоумышленник до поры до времени аккуратен и не меняет содержимого сообщений. Да, известны средства противодействия и этой напасти — например, отправка открытого ключа получателем отправителю по нескольким независимым каналам сразу, включение этого ключа в само сообщение с формированием хеш-суммы полученной комбинации и её последующей сверкой и т. д. Но каждый новый уровень защищённости от MITM увеличивает расходы на передачу данных и снижает её скорость, что для множества реальных приложений неприемлемо.
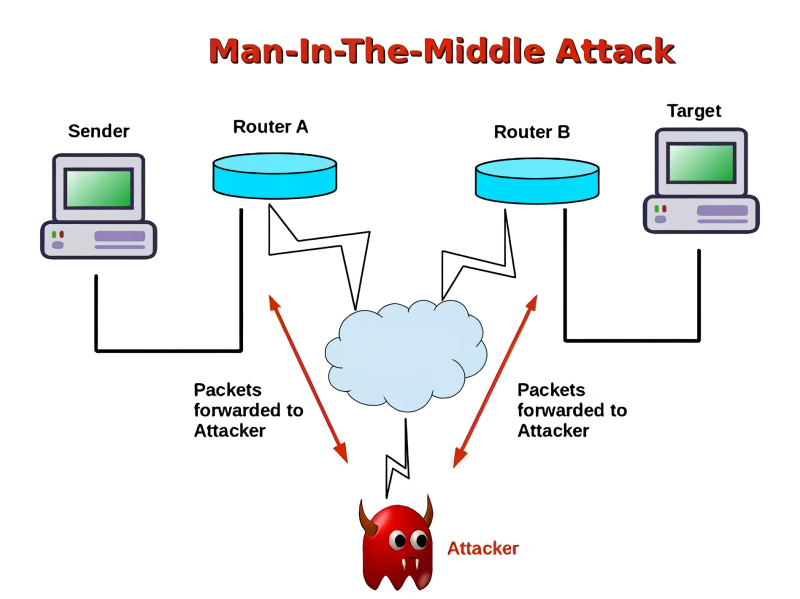
Атака MITM особенно эффективна в случае интернет-коммуникаций, если у злоумышленника имеется возможность перехватить единственный канал связи между отправителем и получателем шифрованного сообщения (источник: The Security Buddy)
Возникает, по сути, тупик: даже имея в своём распоряжении абсолютно устойчивый к попыткам взлома шифр Вернама (математически строго его стойкость независимо доказана советским академиком Владимиром Котельниковым в 1941 г. и американским криптографом Клодом Шенноном, Claude Shannon, создателем современной теории информации, в 1945-м), отправитель и получатель секретного сообщения не могут гарантировать стопроцентную надёжность канала связи, по которому необходимо передать криптографический ключ: даже фельдъегеря можно подкупить, даже одноразовый шифроблокнот скопировать и т. п. Точнее, не могли, пока в дело не вступила квантовая физика — благодаря которой абсолютно защищённые коммуникации всё-таки оказываются возможными. Именно благодаря непривычным с повседневной, макроскопической точки зрения особенностям поведения квантовых объектов становится реальностью создание такого канала коммуникаций, появление MITM в котором в принципе не может остаться незамеченным. А значит, схеме с асимметричным ключом можно доверять, — и это открывает дорогу к применению уже любой сложности гибридных алгоритмов шифрования.
Квантовая криптографическая система в общем случае представляет собой комбинацию двух каналов связи: классического широкополосного, по которому передаётся массив полезных данных в зашифрованном виде, и собственно квантового — для обмена ключами шифрования. Или, как чаще говорят, для распределения этих ключей, поскольку число абонентов кодированных коммуникаций может быть больше двух. Квантовый канал в реализуемых сегодня системах такого рода обычно оптический, а в роли формирующих его квантовых объектов выступают фотоны — которые могут передаваться либо по волноводам (оптоволоконным линиям) между наземными станциями, либо непосредственно через пространство, если речь идёт о воздушных либо спутниковых системах квантовых коммуникаций.
На чём, собственно, основана возможность MITM перехватывать сообщения между легитимными участниками коммуникаций? На том простом факте, что информация в классических каналах связи, где не проявляются квантовые эффекты, с лёгкостью тиражируется, т. е. часть её носителей — тех же самых фотонов в оптоволокне или электронов в кабеле Ethernet — может быть совершенно незаметно для отправителя и получателя отведена в сторону. Более того, при передаче на большие расстояния электромагнитный сигнал затухает, так что его специально усиливают, — и это создаёт дополнительный простор для неприметной активности MITM.

Первая лабораторная установка Беннета и Брассара, подтвердившая возможность квантовой криптографии (источник: Scientific American)
Однако чем слабее сигнал, чем меньше в потоке его элементарных носителей, тем ощутимее становится потеря каждого фотона. Более того, фотоны — кванты электромагнитного потока, его мельчайшие неделимые частицы. Неделимость же их подразумевает, что из однофотонного канала связи в принципе невозможно организовать утечку: один-единственный квант излучения либо доберётся от источника к приёмнику, либо нет. Но если фотон в канале всего один, как можно кодировать информацию, — ведь играть интенсивностью потока уже не получится? Да, но это и не нужно: ведь частица (она же волна, как учит нас корпускулярно-волновая теория) обладает таким, к примеру, квантовым свойством, как поляризация. Квантовые же свойства частиц, как мы уже отмечали в материале о квантовых компьютерах, меняются в зависимости от того, произведено над ними наблюдение или нет. В частности, теорема о запрете клонирования прямо запрещает создание точной копии квантового состояния частицы — в данном случае фотона с определённой поляризацией, — если состояние это априори неизвестно.
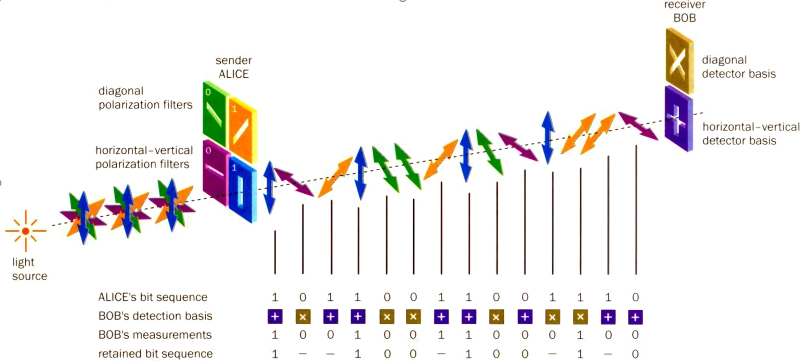
Именно эта идея легла в основу исторически первого протокола квантовой криптографии BB84, предложенного в 1984 г. Чарльзом Беннетом (Charles Bennett) и Жилем Брассаром (Gilles Brassard). Суть его в следующем: отправитель кодирует каждый бит, отправляемый по однофотонному каналу связи, либо вертикально-горизонтальной, либо диагональной поляризацией, причём определённый тип кодировки выбирается для каждого очередного фотона случайно. Получатель же — также случайным образом — использует на своей стороне либо вертикально-горизонтальный, либо диагональный поляризатор для детектирования типа добравшегося до него фотона. Соответственно, примерно в половине случаев получатель фиксирует именно те величины — единицы или нули, — что посылал ему отправитель.
Далее по открытому (неквантовому) каналу производится так называемое просеивание ключа: отправитель сообщает получателю, в какой последовательности он применял поляризаторы при отсылке фотонов в канал, — а получатель, в свою очередь, отвечает, в каких измерениях выбранные уже им состояния поляризаторов совпали с теми, что были у отправителя. Не сообщая притом, единицы или нули он получал в каждом из этих случаев: отправитель ведь и без того знает, что за данные он посылал. Вот эта последовательность верно принятых и полученных битов и образует в итоге ключ — который может быть достаточно длинным.
Если часть фотонов в канале перехватил (и затем переотправил, стремясь не выдать себя) злоумышленник, то вследствие теоремы о запрете клонирования испущенные им взамен оригинальных фотоны неизбежно будут иметь несколько иные квантовые состояния (даже при формально совпадающей с исходной макроскопической поляризацией) — и потому доля совпадений отправленных и полученных данных у легитимных участников коммуникации окажется уже ощутимо меньше 50%. Предельная величина ошибки в ходе передачи сигналов по протоколу BB84, при которой всё ещё возможно получение работающего ключа шифрования, составляет 11%. Она достигается за счёт процедур коррекции ошибок и сжатия ключа — свёртки его по определённому алгоритму с тем, чтобы даже если какую-то часть исходной комбинации нулей и единиц злоумышленник успешно перехватил, в сжатом виде эта часть не превышала бы в идеале одного бита.
Безусловно, в реальной рабочей установке, да ещё имеющей дело с отдельными фотонами (как получать их поток из светового пучка лазера или светодиода — вопрос особый), в любом случае проявятся объективные потери данных, никак не связанные с возможной прослушкой, и чем заметнее расстояние между отправителем и получателем, тем их окажется больше. На сегодня предельное расстояние рабочего плеча постоянно действующей оптоволоконной линии квантовой шифрованной связи (реализованной даже не по BB84, а по более современным протоколам) не превышает 130 км (лабораторный рекорд — около 600 км), в результате чего активный квантовый канал коммуникаций между Пекином и Шанхаем, например, вынужденно содержит целых 32 промежуточных доверенных узла. Впрочем, первая установка Беннета и Брассара, реализованная в 1989 г., обеспечивала связь на расстоянии всего-то 32,5 санитметра, — так что прогресс по этому направлению определённо имеется.
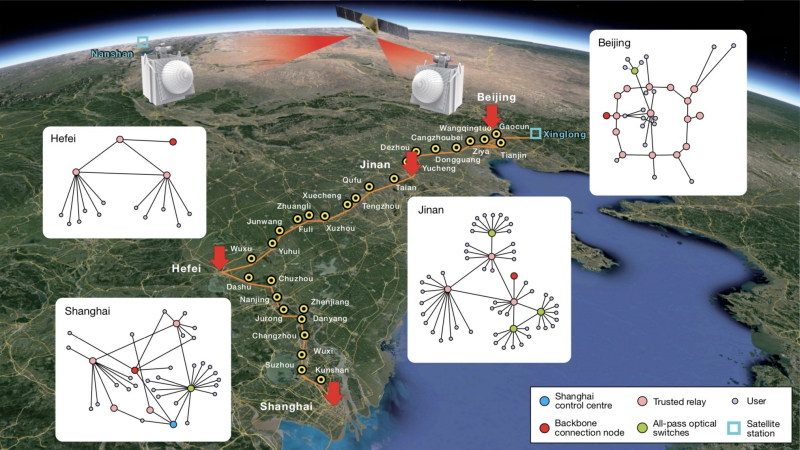
Запущенная в 2021 г. и до сих пор наиболее протяжённая сеть с квантовым шифрованием обеспечивает квантовое распределение ключей на дистанции свыше 4600 км (источник: Nature)
На современном этапе технологического развития квантовая криптография вынуждена принимать в расчёт довольно серьёзное несовершенство реально доступной аппаратуры — что в целом понижает порог уверенности в гарантированном отсутствии вмешательства третьей стороны. Так, вместо (не созданного пока) равномерно испускающего одиночные фотоны источника приходится использовать более или менее стандартные лазеры с последующим ослаблением когерентного пучка — из-за чего уровень неопределённости в ходе генерации ключа возрастает. Ещё один прикладной вопрос, который приходится решать квантовым связистам, — применение аппаратуры, доверия к которой попросту нет, т. е. поставленной разработчиком, имевшим возможность (а то и прямое намерение!) реализовать в ней некие средства потенциального перехвата чувствительной информации. Речь идёт о развитии направлений квантовой криптографии, полностью независимой от аппаратуры (device-independent quantum key distribution, DI-QKD), а также независимой от измерительного оборудования (measurement-device-independent quantum key distribution, MDI-QKD).
С приёмниками одиночных фотонов ситуация также не самая радужная. Поскольку лучший способ минимизировать вмешательство третьей стороны в процедуру квантовой генерации ключа шифрования — это сократить время самой генерации, исследователи стремятся максимально повысить скорость этой процедуры на линии связи. Но быстрое (с частотой около 1 ГГц) и уверенное (со значительно более низким уровнем неопределённости) детектирование единичных фотонов требует сегодня применения сверхпроводниковых датчиков, действующих при криогенных температурах — около 2 кельвин. Поддержание соответствующих температур представляет собой непростую инженерную задачу — тем более если задаться целью сконструировать мобильный (или хотя бы подвижный) терминал криптографической квантовой связи. А ведь нужно помнить ещё и о потенциальной возможности взлома квантовых криптографических систем (методом «ослепления» тех самых высокочувствительных датчиков мощными лазерными импульсами, в частности).
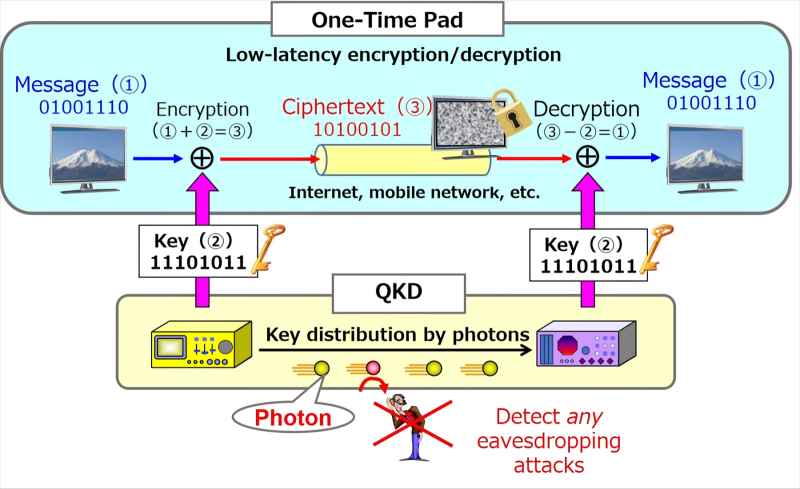
Общая схема передачи шифрованных сообщений по открытому каналу с одновременным квантовым распределением ключей (источник: NEC)
Да и в целом квантовая криптография — вовсе не гарантия обеспечения надёжного канала зашифрованной связи. По сути, такая система лишь позволяет всякий раз с уверенностью утверждать, скомпрометирован или нет очередной сгенерированный для обмена данными ключ шифрования. Если же злоумышленник ставит своей целью не перехват чувствительных данных, а лишение легитимных участников коммуникации возможности эффективно обмениваться ими, то цели своей он достичь сумеет.
Так в чём же тогда принципиальное преимущество квантовой криптографии перед классической? Прежде всего — в явной ориентации на работу с открытыми каналами связи (после успешной генерации ключа шифрования), в высокой степени автоматизации самой процедуры формирования ключа, а также в возможности часто и быстро менять такие ключи — фактически действуя в режиме старого доброго шифроблокнота с уникальными кодами, только непрерывно обновляемого и почти не поддающегося взлому (со всеми вышеуказанными оговорками). Здесь важно понимать, что квантовая криптография обеспечивает достаточный уровень конфиденциальности: если вся аппаратура работает штатно, если в ходе генерации ключа шифрования не было зафиксировано превышения предельно допустимого уровня ошибок — то можно практически со стопроцентной уверенностью гарантировать, что компрометации канала связи не произошло. Уже одно это дорогого стоит.
Важно также, что помимо соединений «точка-точка» квантовая криптография работает и в конфигурации «звезда» — когда один из узлов защищённой сети принимает на себя функции сервера и, соответственно, хранит все ключи шифрования, сгенерированные в ходе взаимодействия с подключёнными к нему клиентскими узлами. Этот своего рода «квантовый телефон» доведён в России до уровня предсерийного образца ещё в 2019 г. компанией «ИнфоТеКС» и Центром квантовых технологий физического факультета МГУ имени М. В. Ломоносова. Та же компания, кстати, в середине 2023-го получила сертификаты ФСБ России для квантовой криптографической системы выработки и распределения ключей ViPNet Quantum Trusted System Lite, созданной для обеспечения квантовозащищёнными ключами средств криптографической защиты информации в автоматическом режиме.
И всё же никакие «квантовые телефоны» и иные устройства, базирующиеся на принципе квантовой генерации ключа, не будут иметь смысла в том случае, если базовый алгоритм шифрования — тот самый, для которого этот ключ требуется, — сам потеряет актуальность вследствие скачкообразного роста возможностей вычислительных систем. Несколько ранее мы уже упоминали о квантовых компьютерах, развитие которых до мощности примерно в 1 тыс. согласованно действующих кубитов позволит просто методом грубой силы решать многие математические проблемы — в том числе и те, что лежат в основе ряда популярных алгоритмов шифрования. Многие, но, к счастью, не все.
Алгоритмы с открытым ключом, в частности относящиеся к семейству RSA, падут, увы, одними из первых, — поскольку как раз им угрожает предложенный в 1994 г. алгоритм Шора для факторизации больших чисел. Чем больше число взаимозапутанных логических кубитов (чрезвычайно важно не путать их с физическими — об этом мы подробно говорили в статье, на которую только что дали ссылку) в квантовом компьютере, тем скромнее значение ошибки производимых им вычислений. И тем, получается, меньше погрешность при вычислении закрытого ключа на основании открытого — вычислении, перед которым современные суперкомпьютеры в попытке взломать протокол шифрования RSA откровенно пасуют.
В 1996 г. тучи начали сгущаться и над симметричным шифрованием. Лов Гровер (Lov Kumar Grover), работающий в США индийский математик, предложил названный его именем квантовый алгоритм для решения задачи перебора — то есть для поиска ответа на некоторую абстрактную задачу, заданную в виде булевой функции от любого числа переменных. Если это число равно n, то в соответствии с теорией вероятностей количество вариантов перебора N определяется по формуле 2n, — и как раз по этой причине симметричные алгоритмы с длиной ключа в несколько сотен символов так уверенно сопротивляются попыткам подобрать к ним ключ «грубой силой» на фоннеймановских компьютерах. Алгоритм же Гровера сводит задачу перебора на квантовом компьютере к числу операций, пропорциональному квадратному корню из N с близким к единице коэффициентом (т. е. речь идёт уже о двойке в степени n/2), — правда, лишь в том случае, когда количество кубитов в системе велико по сравнению с n. Именно по этой причине для RSA-шифров с ключами в сотни символов длиной подлинную угрозу будут представлять квантовые компьютеры в тысячи логических кубитов — а до выхода таких устройств из стен исследовательских лабораторий пройдёт ещё немало времени.
Конечно, даже это не «серебряная пуля» для цифровой криптографии: широко распространённые сегодня блочные шифры вроде AES и после запуска в серию тысячекубитовых квантовых вычислителей не потеряют своей актуальности. Просто придётся ради сохранения их криптостойкости на прежнем уровне значительно увеличить длину ключа шифрования. Другое дело, что до закодированных ранее с применением, допустим, AES-256 секретов окажется гораздо проще добраться, — возникает опасность так называемых отложенных атак. Уже не первый год и спецслужбы в различных странах, и группировки киберзлоумышленников, и иные интересующиеся стороны накапливают огромные массивы выловленных в Сети зашифрованных данных — с тем, чтобы, как только подвернётся первая же возможность, извлечь из них некую ценную информацию. В опубликованном в мае 2022 г. отчёте-рекомендации McKinsey о подготовке к постквантовой криптографии указывается, что уже в обозримой перспективе заинтересованным государственным и бизнес-структурам следует активно переходить на доступные квантовостойкие решения безопасности (грубо говоря, наращивать длину ключей RSA от минимально рекомендованного ныне нижнего порога в 2048 символов), а к 2030-му — и вовсе мигрировать на более зрелые постквантовые решения.

Квантовый компьютер на ионных ловушках с теоретически неограниченным потенциалом масштабирования по числу кубитов может сам стать эффективным средством для зашифровки (но не декодирования!) постквантовых криптографических сообщений (источник: Universal Quantum)
Общая идея постквантовых алгоритмов шифрования заключается в том, чтобы подобрать такие вычислительно сложные математические задачи, которые, с одной стороны, были бы удобны на практике для реализации на обычных фоннеймановских системах, а с другой — не предусматривали бы известного сегодня решения ни классическими, ни квантовыми методами. Такого рода алгоритмы можно классифицировать следующим образом:
- основанные на многочленах от многих переменных, а именно на системах нелинейных уравнений над конечным полем (плюсы: сравнительно высокая эффективность реализации, скромная длина подписи, значительная длина ключей; минус: заведомо известная внутренняя структура, что потенциально упрощает поиск решения),
- основанные на кодах, исправляющих ошибки, в частности на задаче декодирования произвольного линейного кода (плюсы: относительно высокая эффективность, значительная устойчивость к попыткам найти алгоритмическое решение — по меньшей мере упорно предпринимаемым с 1978 г.; минус: большая длина ключей),
- основанные на теории целочисленных решёток (плюсы: умеренная длина ключа, достаточно высокая эффективность; минус: ощутимая вероятность некорректного декодирования легитимным участником процедуры),
- основанные на криптографических хеш-функциях (плюсы: короткие ключи, высокая уверенность в надёжности решения; минус: возможность обнаружения в будущем алгоритмического средства обращения данной конкретной хеш-функции),
- основанные на изогениях суперсингулярных эллиптических кривых (плюсы: короткие ключи, компактные зашифрованные сообщения; минусы: сравнительно низкое быстродействие, показанная на практике подверженность эффективным атакам).
И это только начало: со временем математики, безусловно, смогут предложить и другие классы вычислительно сложных задач, пригодные для реализации новых постквантовых алгоритмов шифрования.
Уже несколько тысячелетий продолжается состязание тех, кто стремится сберечь свои записанные секреты, с теми, кто намерен во что бы то ни стало до них добраться, — и можно не сомневаться, что по мере дальнейшего развития технологий придётся снова и снова обновлять требования к надёжности криптографических систем. И деваться тут некуда: без эффективной, надёжной и общедоступной криптографии само функционирование цифрового пространства, в которое все мы сегодня в большей или меньшей степени погружены, попросту непредставимо.